Octaholohedron
octa (8) - holo (3-Dimensional) - hedron (multi-sided geometric figure)

The Octaholohedron has often been called a Tesseract. I'm not sure why, because that's not a very appealing name. It is also called the 8-Cell, where a "cell" refers to a 3-Dimensional solid. It is made from 8 Cubes, each meeting at a square face, and each rotated 90° to his neighbors. It's composition in 4 dimensions is very similar to that of a Cube in 3 dimensions - just as a Cube is similar to a Square. It is made from 16 points using the formula (±d, ±d, ±d, ±d) where d is half the length of a side. On this shape there are 24 square faces where the cubes meet, 32 edges, and 16 points.

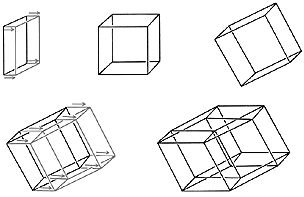
The octaholohedron is probably the easiest to understand of the 4-D solids. It's creation is visually straightforward:

• start with a line of length s
• copy and move it a distance s at 90° to the original line to make a square
• copy and move the square up a distance s at 90° to the original square to make a cube
• now, copy and move that cube a distance s in the 4th Dimension, at 90° to the original cube making an Octaholohedron!

Here is a picture of the Square-to-Cube and the Cube-to-Octaholohedron process:

Here's another picture of an Octaholohedron: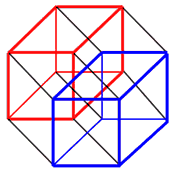

Remember: an octaholohedron is a 4-Dimensional object, and it has a 3-Dimensional shadow. This is a flattened view of it's shadow.
One of the cubes is outlined in blue, and the cube opposite it is outlined in red. The other 6 cubes have 1 red-lined face, 1 blue-lined face, and 4 black-lined faces. Can you spot all 8 cubes?

I always remember first seeing this shape as a cube within a cube with points connected, and not understanding why. Scientists always said, "this is it, a cube in a cube." An octaholohedron is not a cube in a cube though. The outer cube is closer to us in the 4th dimension, while the smaller cube is farther away - they don't even touch each other. The difference in size is caused by exaggerated perspective. Just in case you haven't, see if you can figure out when a cube would look like a square in a square with points connected.

RETURN