Tetricosiholohedron
tetra (4) - icosi (+20) - holo (3-Dimensional) - hedron (multi-sided geometric figure)

The Tetricosiholohedron was my first pet project. At first, I knew this shape was made from Octahedra, but I didn't know how many, or how they were arranged. To figure out how this shape was made I built an unfolded Tetricosiholohedron (an idea I first got while designing the Hexideciholohedron) in 3 dimensions (this is similar to drawing squares on a piece of paper so thay could be cut out and folded into a square). I started by making a lot of octahedrons out of paper. I then glued them together and marked which faces corresponded with each other. When I finished, I had an interesting sculpture made of 24 Octahedra, if you would like to see what it looks like, Click Here.

After this, I proceeded to plot the points out on a piece of paper, and that's when the surprise hit me - its points are the same as the Octaholohedron's and Hexideciholohedron's points combined! I'll bet this makes for some fun and interesting puzzles in a 4-D Student's Geometry Class.

I found that this 4-D shape is made from 24 Octahedra, 96 Triangles, 96 Lines, and 24 Points.
16 of the points are the same as those on an Octaholohedron, and the other 8 are the same as those on a Hexideciholohedron. One Octahedron corresponds with each square face of an Octaholohedron. Also of interest, 6 Octahedra meet at each point in a cubical arrangement (this must be, because the cross section of an Octahedron near a point is a square - 4 Triangles meet in a square arrangement).

Graphed out and shown on 2-D paper, and with a little perspective, it looks like this:

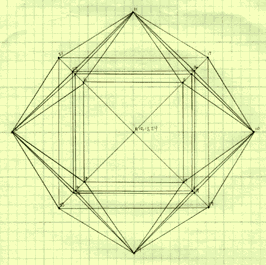
You can readily see 4 Octahedra circling the outside edge, while the rest of the Octahedra overlap or obscure each other. Remember, 6 Octahedra meet at each point, and there are 4 points in the center.

And here is a computer generated line drawing, try to identify some octahedrons in this...

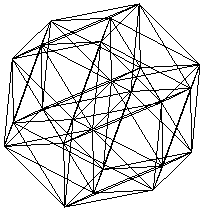
This shape doesn't correspond with any of the 3-D perfect solids. Depending on rotation, its cross-sections look like the Cuboctahedron, the Rhombic Dodecahedron, a Hexagonal DiFrustum (a Frustum is a pyramid with the top point cut off), and an Elongated Hexagonal DiPyramid. (pictures of these should be available soon) This shape is obtained from an Octaholohedron and a Hexideciholohedron in almost the same way that the Cuboctahedron and the Rhombic Dodecahedron are obtained from the Cube and Octahedron, so those are the two shapes I usually associate with it.

After figuring out this shape, I took the points, rotated them, added 4-D perspective, and then built a 3-D model of its shadow out of string! To see some pictures of it, Click Here!

RETURN